用dfa的角度去看待kmp算法——dfa的构造过程

本文可以算是《算法》（中文第四版）p499-501的一个小笔记。

纠结了一个星期的kmp总算是看下来了（虽然没有完全看懂）

废话少说，直接开始笔记。

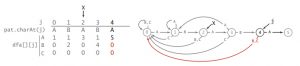
DFA全程是「确定有限状态自动机」，在《算法》第四版中，采用了一个dfa数组建立一个确定有限状态自动机，并利用这个数组实现了状态间的跳转。

上图会好理解一点。

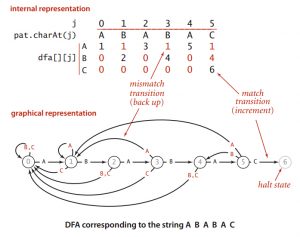
这个图的下半部分就是以「ABABAC」为目标字符串而建立的dfa。

圆圈可以被称为第j个状态，也就是匹配了j个字符后字符串处于的状态。匹配到1个字符就+1，然后进入状态1，再匹配到一个字符就再+1，然后进入状态2。

比如说，现在输入了ABAB，则进入了第【4】状态，如果我再输入一个「A」，那我就可以进入第【5】状态。如果我输入的是「B」或者「C」，就会回退到之前的状态，在这里无论是输入「B」还是「C」都会回退到第0状态（匹配到0个字符，也就是没有匹配到任何字符，重新开始）。

而dfa[c][j]的定义是：

你现在已经处于第【j】个状态，你输入的下一个字符是「’c’」后进入的状态。

 

比如说，一开始我们没输入任何字符，所以我们处于状态【0】。在输入「B」或「C」之后，因为目标字符串的第一个字符是「A」，不匹配，所以我们还是会进入状态0；而在输入「A」之后，因为匹配，所以会进入状态【1】。

在图中，黑色代表匹配成功，进入下一个状态；红色代表匹配失败，进入现在和前面之中的某一个状态。

以此类推，如果我们的输入（即使还没输入完）能够使dfa达到最后一个状态（即状态【6】，匹配完成的状态），则字符串匹配成功，否则匹配失败。

 

也就是说，这个算法的关键在于构建dfa二维数组。

 

那么问题来了，dfa二维数组要怎么构建？

这就是今晚我思考了很久才想通的问题。

 

 

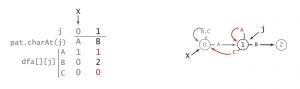
构建dfa的代码如下（java）：

dfa[pat.charAt(0)][0] = 1;
for(int X = 0, j = 1; j < M; j++) {
// 计算dfa[][j]
for(int c = 0; c < R; c++) {
    dfa[c][j] = dfa[c][X];
}
    X = dfa[pat.charAt(j)][X];
}

 M是输待匹配字符串（输入）的大小，pat是目标字符串（pattern），R是所使用的字符集的大小（例如说如果是ASCII码则为128）。

而X是创建dfa过程中的一个重要变量。这个X就是本文要研究的重点，也是迷惑了我一晚上的东西。

我们先来看一个例子。

本例中目标字符串是「ABABAC」，假设我们的输入是「ABABABAC」，那么，当j = 5时（字符串的第一个字符时j = 0），我们已经进入了第【5】状态（已匹配了5个字符，「ABABA」），但下一个字符，「B」和「C」不匹配。所以，此时我们应该回退到第【k】状态（k <= 5），从上面的DFA图我们可以看到，我们要进入第【4】状态（匹配了「ABAB」），即dfa[‘B’][5] = 4。

那么dfa[‘B’][5] = 4是怎么得出来的？其实是通过前面的情况递推出来的。

 

我们先看初始情况：

很明显，对于dfa[ ][0]来说，因为是第0个状态，所以只有待匹配字符串的第一个字符和目标字符串的的第一个字符相同时，才可以进入下一个状态。所以dfa[pat.charAt(0)][0] = 1，其他dfa[ ][0] = 0。

那么问题来了，我们知道了初始情况，那我们怎么从初始情况推理去剩下的情况？

 

在这里，我们就需要引入一个大杀器，那就是X。

https://book.douban.com/subject/19952400/discussion/59623403/   ←关于X的详细解释。

我们引入一个状态数组X，X[j]是正确输入pat[1 .. j-1]后进入的状态，所以输入p[1 .. j-1]c（c != p[j]）后，进入的状态就是dfa[c][x[j]]（在X[j]状态下输入c），即dfa[c][j] = dfa[c][x[j]]。

那么X数组怎么求？用递推。

X[k + 1]为正确输入p[1 .. k]后进入的状态，即正确输入p[1 .. k-1]p[k]后进入的状态。即在输入了p[1 .. k-1]后输入p[k]的状态，即dfa[p[k]][x[k]]。

所以X[j + 1] = dfa[pat.charAt(j)][X[j]];

由于Ｘ是个递推用的辅助变量，所以我们可以只保存它上一次存储的值。

可以理解Ｘ的意义为：当下一次匹配失败时，与现在这个状态等价的状态。

 

 

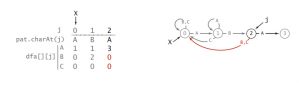
还是刚才那个例子，我们的目标字符串是「ABABAC」，而我们的输入是「AA」，会怎么样？很明显，此时j = 1，「A」和「B」不匹配。

除此之外我们目前还掌握着什么信息？

1. 因为匹配已经失败，所以我们不能以输入的开头作为匹配开头。
2. 同理，txt.charAt(j) != pat.charAt(j)
3. 在 1 ~ j-1这个范围内，它们是匹配的

所以我们可以直接放弃最开始的A，把我们的输入当做「A」（因为以最开始的A为开头已经不可能匹配到目标字符串）。那么，输入「AA」和输入「A」后进入的状态是一样的。所以dfa[‘A’][1] = dfa[‘A’][0];

就这样，我们把未知的东西转换成了我们已知的东西。用数学归纳法的语言来讲，就是找到了从k递推到k+1的方法。

 

（感觉其实也还没说清楚，可是现在真的晚了，还是等看懂了再继续写吧）

 

---

2018.8.20更新：

又重新看了一遍，总算是真正搞懂了X的意思以及为什么会有dfa[c][j] = dfa[c][x]这一步……

X是输入[1 .. j-1]（以0开头已匹配不到且第j个匹配失败）后所能到达的状态。

然后，要记住dfa[][]中的是下一个会进入的状态。而不是本次进入的状态。

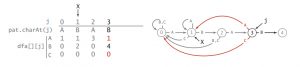
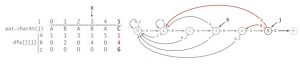
还是举一下刚才那个例子。模式为ABABAC。

我们现在有初始情况 dfa[][0]，除了dfa[A][0]其他都为0，怎么推导出dfa[][1]？

因为我们知道匹配成功时的情况（dfa[B][1] = 2），所以我们只需要考虑匹配失败的情况。

当j = 1时，[1 .. j -1]为空集（AX(X为使匹配失败的字符)之间没有任何字符）。也就是说，无论是AA还是AC，如果匹配失败，都和没有输入字符的情况等价，也就是，和初始情况等价。所以初始化X = 0，dfa[c][j = 1] = dfa[c][X  = 0]。

然后考虑j = 2时的推导，同样，我们只需要考虑匹配失败的情况。此时[1 .. j-1] = [1] = B，所以匹配失败的情况下，输入ABX与输入B进入的状态是一样的。那我们要怎么更新X为输入B之后进入的状态？

回顾之前dfa的定义，dfa[c][j]为在状态j下输入c，上一轮的X的状态为空，即没有输入任何字符。所以我们要做的只是把B输入进去，更新X的状态。

所以 X = dfa[pat.charAt(j)（此时为B）][X]。这样X就更新为输入了B的状态。

（做一个补充说明，因为是在本轮循环的最后更新X，用于下一轮使用，所以X = dfa[pat.charAt(j)][X]而不是 j -1）

然后再进行dfa[][j] = dfa[][x]，把失败的情况复制进去。

 

再接下来也是如此，下一轮的[1 .. j-1] = BA，要更新X，我们只需要把A输入进去就行了，代码同样也是X = dfa[pat.charAt(j)（此时为A）][X]

 

因为X <= j，所以当我们要更新X时，它要进入的下一个状态肯定是已经推导出来的。

大概就是这样了……